Опыт 3.

«Гармонические колебания пружинного маятника»

 Пружинный маятник — представляет  собой механическую систему, состоящую из пружины и груза, соединенного с этой пружиной.  Пружинный маятник может быть расположен вертикально, горизонтально или под углом к горизонту.

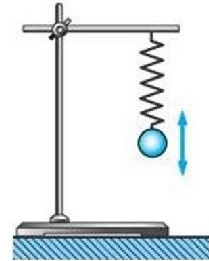
 Прибор пружинный  маятник,  состоит из штатива со стержнем, на который подвешивается пружина с грузом ( рис.1 ).

 Обычно маятник неподвижен и груз находится в положении равновесия.    

Рис.1.

Опыт 1. Если  груз  отклонить ( например вниз) от положения равновесия, то он начнет совершать вертикальные колебания под действием силы тяжести и силы упругости пружины.

Проблема. Какое движение совершает пружинный  маятник во время колебательного движения  ?                                                                                                       

Рис. 2.

Ответ. Рассмотрим установку, представляющую пружинный маятник   с полым конусом вместо тела ( рис.2). 

 Внизу находится лист картона, на который будет высыпаться песок из конуса маятника.. 

·        Пусть лист картона находится в состоянии покоя. Насыплем в конус пружинного маятника песок и закроем нижнее отверстие, чтобы песок не высыпался. Отведем маятник вправо и откроем отверстие. Маятник начнет колебаться, а песок высыпаться. Так как лист картона находится в покое, то песок, высыпаясь из конуса,  будет вычерчивать прямую линию. По этой прямой линии невозможно выяснить характер движения пружинного маятника.

·        Отведем маятник вправо и откроем отверстие. Маятник начнет колебаться, а песок высыпаться. Приведем лист картона в равномерное движение так, как это показано на рисунке.                                       

·        Рисунок будет иллюстрировать характер колебания маятника. Этот рисунок называется графиком колебания   математического маятника. Такой график называется синусоидой.

·        Если какое либо тело колеблется по синусоидальному закону, то такое колебание  называется гармоническим. Смещение при колебании груза на пружине будет определяться формулой :

Х = Х₀ sin ω t 

Вывод :

« Колебания пружинного маятника являются гармоническими, так как они совершаются по синусоидальному закону ».

Опыт 4.

«Законы колебания пружинного маятника»

 Основной характеристикой пружинного маятника является период колебаний, поэтому в  данном исследовании выясним, как зависит период колебаний пружинного  маятника от амплитуды колебаний, от массы груза пружинного маятника, от жесткости пружины.

 Соберем установку на рис.1.

Рис.1.

Опыт 1. Выясним зависимость периода колебаний пружинного маятника от амплитуды колебаний.

Проблема. Как это сделать ?

Ответ. Отклоним маятник от положения равновесия на небольшую высоту и отпустим. Маятник будет совершать гармонические колебания. Определим период колебаний Т₁. Проделаем несколько таких опытов, каждый раз увеличивая амплитуду колебаний и определяя Т₂, Т₃ и т.д.

Окажется что Т₁ = Т₂ = Т₃

Вывод -  Период колебания пружинного маятника                                                         

не зависит от амплитуды колебаний.

 Опыт 2. Выясним зависимость периода колебаний математического маятника от массы  груза маятника..

Проблема. Как это сделать ?

Ответ. Отклоним маятник от положения равновесия на небольшую высоту и отпустим. Маятник будет совершать гармонические колебания. Определим период колебаний Т₁. Прикрепим к к грузу маятника дополнительные грузы и определяя Т₂, Т₃ и т.д.

После проведения опытов и построения графика окажется, что Т ~ √ m

Вывод -  Период колебания пружинного маятника  зависит от массы маятника  Т ~ √ m.

 Опыт 3. Выясним зависимость периода колебаний математического маятника от жесткости пружины.

Проблема. Как это сделать ?

Ответ. Отклоним маятник от положения равновесия на небольшую высоту и отпустим. Маятник будет совершать гармонические колебания. Определим период колебаний Т₁. Заменим  пружину маятника  на пружины,  с другой жесткостью, определяя при этом периоды колебаний нити Т₂, Т₃ и т.д. Период колебаний в каждом случае будет разным..

После проведения опытов и построения графика окажется, что Т ~ √ 1/ к

Вывод -  Период колебания пружинного маятника  зависит от жесткости пружины  маятника  Т ~ √ 1/к.

Объединяя результаты опытов 2 и 3,  получаем формулу периода пружинного маятника ( рис.2).

Рис. 2.

Во время колебаний пружинного маятника происходят непрерывные превращения энергии ( рис.3) – потенциальная энергия переходит в кинетическую и наоборот. Если бы не было трения в подвесе и сопротивления воздуха, то не было бы потерь энергии, и маятник колебался бы вечно.                           

                                                                                                                                                                           Рис.3.